1. Background
Surface/interfacial energies play a very important role in various industrial processes, such as mineral separation, oil sands separation, wastewater treatment, pulp and paper making, surface coating, painting, etc. Surface and interfacial properties can be conventionally measured using drop methods (sessile drop method and pendant drop method) and probe methods (Du Noüy ring method, Du Noüy-Padday rod method and Wilhelmy plate method).
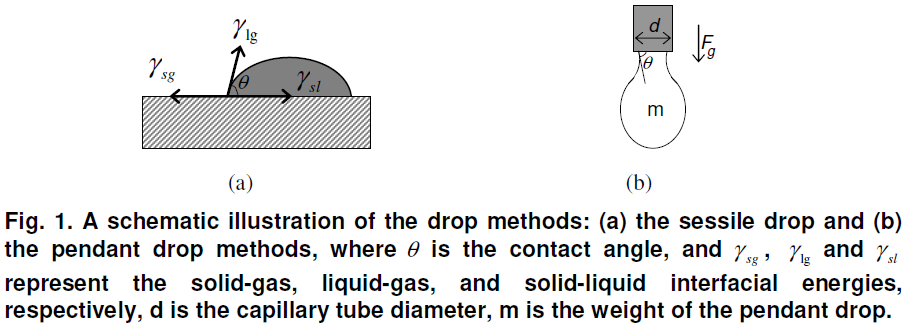
The sessile drop method is used for the characterization of solid surface energies, and in some cases, aspects of liquid surface energies as shown in Fig. 1(a). The shape of a liquid-vapor interface is determined by the Young-Laplace equation, with the contact angle playing the role of a boundary condition via Young’s Equation. The shape profile of the sessile drop is digitized and analyzed using the Young-Laplace equation for contact angle calculation
.
Surface/interfacial energies play a very important role in various industrial processes, such as mineral separation, oil sands separation, waste water treatment, pulp and paper making, surface coating, painting, etc. Surface and interfacial properties can be conventionally measured using drop methods (sessile drop method and pendant drop method) and probe methods (Du Noüy ring method, Du Noüy-Padday rod method and Wilhelmy plate method)
If the solid-vapor interfacial energy is denoted by, γsg , the solid-liquid interfacial energy by, γsl , and the liquid-vapor interfacial energy (i.e. the surface tension) by, γlg , then the equilibrium contact angle, θ , is determined from these quantities by Young’s Equation:
![]()
The main premise of the method is that by placing a drop of liquid with a known surface energy, the shape of the drop, specifically the contact angle, and the known surface energy of the liquid are the parameters that can be used to calculate the surface energy of the solid sample. The liquid used for such experiments is referred to as the probe liquid, and the use of several different probe liquids is required.
The pendant drop method is a technique by which a drop of liquid is suspended from a tube (capillary or needle) in a bulk liquid or gaseous phase. The shape of the drop results from the relationship between the surface tension or interfacial tension and gravity. In the pendant drop method, the surface tension or interfacial tension is calculated from the shadow image of a pendant drop using drop shape analysis in accordance with the Young-Laplace equation as shown in Fig. 1(b). The force due to surface tension is proportional to the length of the boundary between the liquid and the tube, with the proportionality constant usually denoted. Since the length of this boundary is the circumference of the tube, the force due to surface tension is given by, Fγ=πdγ , where d is the tube diameter, π = 3.14159.
The mass, m, of the drop hanging from the end of the tube, can be found by equating the force due to gravity with the component of the surface tension in the vertical direction giving the formula,
![]()
where θ is the contact angle with the tube, and g is the acceleration due to gravity. The limit of this formula, as θ goes to 90°, gives the maximum weight of a pendant drop for a liquid with a given surface tension, γ .
![]()
This relationship is the basis of a convenient method of measuring surface tension. More sophisticated methods are available to take account of the developing shape of the pendant as the drop grows.
The du Noüy ring method is one technique by which the surface tension of a liquid or the interfacial tension between two liquids can be measured as shown in Fig. 2(a). The method involves slowly lifting a ring, often made of platinum or platinum-iridium, from the surface of a liquid. The material is also chemically inert and easy to clean. The force, F, required to rise the ring from the liquid’s surface is measured and related to the liquid’s surface tension, γ.
![]()
where Rj is the radius of the inner ring of the liquid film pulled and Ra is the radius of the outer ring of the liquid film.
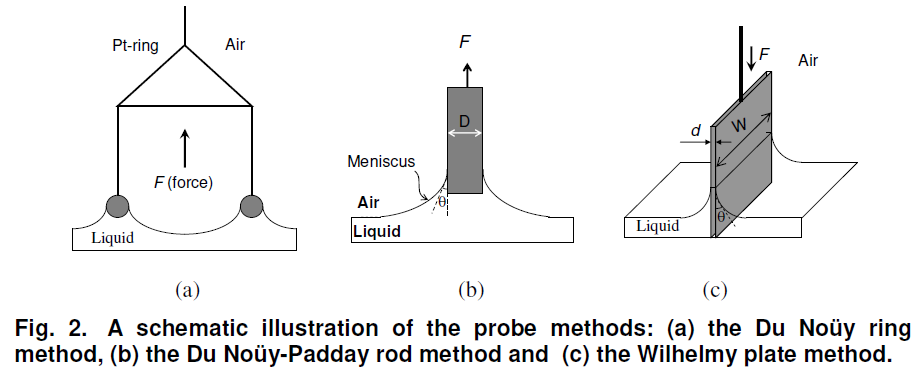
The Du Noüy-Padday rod method is a minimized version of the Du Noüy ring method replacing the large platinum ring with a thin rod (probe) that is used to measure equilibrium surface tension or dynamic surface tension at an air-liquid interface. The rod is attached to a scale or balance via a thin metal hook. The Padday method uses the maximum pull force method, i.e. the maximum force due to the surface tension is recorded while the probe is first immersed approximately one mm into the liquid and then slowly withdrawn from the interface.
![]()
where D is diameter of the probe, γ is the surface tension of the liquid. The maximum pull force is obtained when the buoyancy force reaches its minimum. This is observed as a maximum in the force curve, which relates to the surface tension
Wilhelmy plate method is used to measure equilibrium surface and interfacial tension at an air-liquid or liquid-liquid interface as shown in Fig. 2(c). In this method, the plate is oriented perpendicular to the interface, and the force exerted on it is measured. The Wilhelmy plate is often made from filter paper, glass or platinum which may be roughened to ensure complete wetting. In fact, the results of the experiment do not depend on the material used, as long as the material is wetted by the liquid. The plate is cleaned thoroughly and attached to a balance with a thin metal wire. The force on the plate due to wetting is measured using a microbalance and used to calculate the surface tension,, using the Wilhelmy equation
![]()
where l is the wetted perimeter (2w + 2d, w is the plate width and d is the plate thickness) of the Wilhelmy plate and θ is the contact angle between the liquid phase and the plate.
2. Multi-channel tensiometer
Fig. 3 is an illustration of the measuring process for a single sensor. Multiple sensors are arranged in parallel and automatically controlled for a multi-channel tensiometer, which is a bonus function of the multi-channel scanning water analyzer.
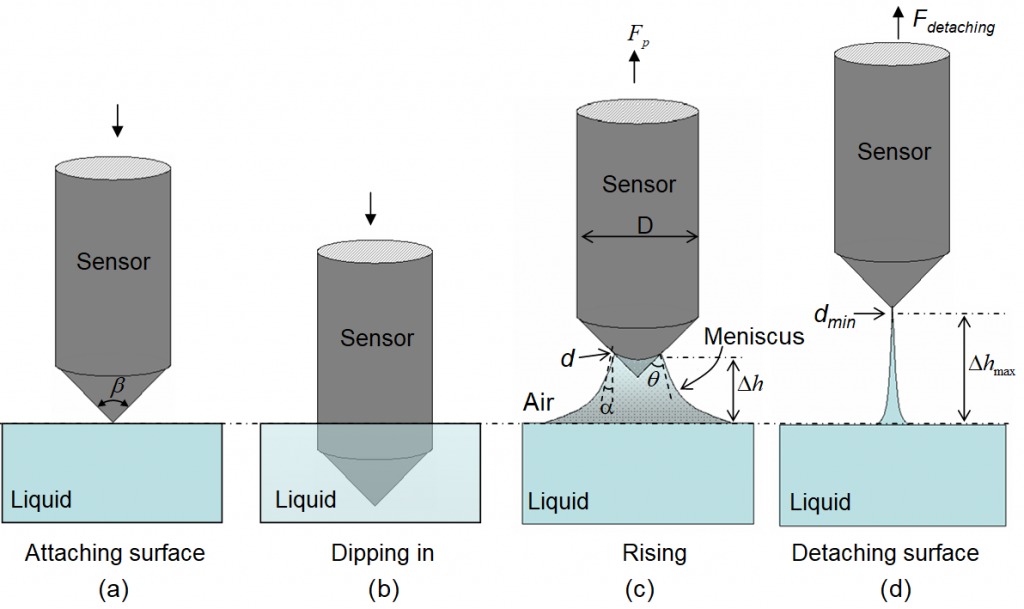
Fig. 3. An illustration of the measuring process.
In a measurement scan, the sensors move down from one medium (e.g. the air for surface tension or a liquid for interfacial tension) and dip in another liquid medium and hold in the liquid medium for a short time period and then rise up to its original position. During the sensor rising period, the excessive force that needs to pull the sensor up is equal to the weight of the meniscus pulled up above the reference level. The reference level is the flat meniscus before the sensor’s contact with the liquid. If the sensor tip is at a distance Δh above the reference level then the excessive vertical pulling force, Fp , can be expressed as
![]()
where γ denotes the interfacial tension between the liquid and the surrounding medium, πd denotes the wetted perimeter and d the wetted diameter, and α is the angle between the liquid and the gravity direction, which can be calculated using
![]()
where θ is the contact angle between the liquid and the sensor’s cone surface, β is the cone shape angle. The second part of equation (7) represents the net gravitational force excluding the buoyancy, where Vm is the volume of the meniscus pulled up above the reference level, ρ1 and ρ2 are the densities of the two media, g the gravitational acceleration constant.
Considering the cone-shaped tip that makes the meniscus as an elastic thin liquid string during pulling, the gravitational part is a few orders of magnitude below the first surface tension part, hence equation (7) can be rewritten as,
![]()
For the sensor rising period, the excessive pulling force on the sensor is approximately proportional to the height of the meniscus as the blue curve shown in Fig. 4, which is an illustration of the response signals representing capacitance change, C(t) , and its derivative, C'(t) , as well as inserted excessive pulling force, Fp , as a function of time.
![]()
where k is a sensor constant.

Combining equations (9) and (10), the excessive pulling force on the sensor at the detaching point, Fdetaching, can be given as below,

where dmin is the minimum diameter of the liquid medium relating to the sensor, which is a characteristic of the sensor, depending on the surface roughness and the angle sharpness of the cone-shipped sensor tip. Δhmax is the maximum height of the meniscus at the minimum wetting diameter, dmin. The meniscus liquid string will break or rupture if the sensor is further pulled up. Rearranging equation (11) the surface tension γ can be obtained,
![]()
Δhmax can be derived via numerical data processing using recorded capacitance change, C(t) , and its derivative function, C'(t) . The coefficient, k/πdmin , can be obtained using a reference liquid with known surface tension, such as water for aqueous systems, and xylene for hydrocarbons.
The capacitance change, C(t), of the sensor shows a sharp increase/decrease at the attaching and detaching points, which are identified by the maximum and minimum points (tmax and tmin) of its derivative function, C'(t), as illustrated in Fig. 4. Each sensor tip’s vertical position at the attaching point, p(tmax) and the detaching point, p(tmin), can be obtained numerically via a linear interpolation using recorded tip position function, p(t), Δhmax can then be found by
![]()
Figs. 5 and 6 are the actually scanned curves using an 8-channel tensiometer representing capacitance changes, C(t), and its derivative function, C’(t), for de-ionized water and 0W-20 engine oil , respectively. Eight surface tension values of 8 samples can be obtained in one test run.

Fig. 5. Actual scanned curves of capacitance change C(t) and its derivative C'(t) for de-ionized water using a 8-channel tensiometer .
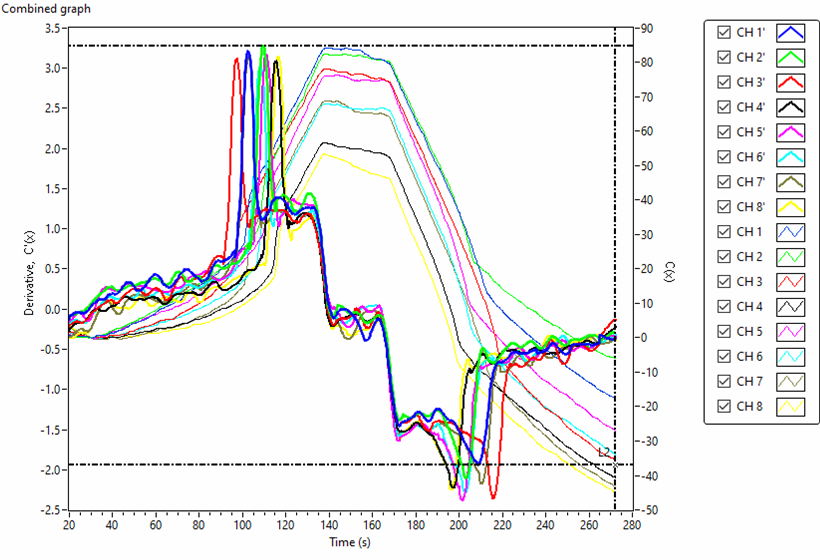
Fig. 6. Actual scanned curves of capacitance change C(t) and its derivative C'(t) for 0W-20 engine oil using a 8-channel tensiometer .